| | |
Использование информационных технологий при решении задач на уроках математики, для развития творческого мышления школьников
Нынешнему поколению учащихся предстоит жить и работать в третьем тысячелетии, когда новые технологии на производстве и в обществе получат своё дальнейшее развитие, поэтому развитие логичного, системного, алгоритмического стиля мышления становится одним из основных направлений в обучении. Всё это требует отличного курса математики. Именно математика даёт возможность развивать критическое мышление у школьников, умение рассуждать и нестандартно действовать в сложных ситуациях, знание, что многие вещи можно доказывать, а не брать на веру. Математика нужна не как шкатулка малонужных знаний, а как школа рационального мышления. Однако при изучении отдельных тем на уроках математики в старших классах, при решении некоторых задач, громоздкие вычисления (как, например, при решении уравнений методом деления отрезка пополам), трудности при построении графиков функций, если сам график не является целью решения, затмевают существо математической задачи, не дают увидеть красоту, рациональность применяемого метода решения.
Целесообразное использование информационных технологий при изучении отдельных тем математики в старших классах помогает в решении вышеизложенных проблем.
В настоящее время актуальным направлением в образовании является разработка и проведение интегрированных курсов и межпредметных уроков, что при условии методически грамотного и содержательного подхода позволяет повысить порог восприятия учащихся и закрепить умения и навыки по предметам и самой информатики.
Существует целый ряд программ по математике, с помощью которых можно не просто поддерживать базовый уровень учащихся, но и существенно корректировать его, повторяя пройденное на новой ступени понимания, а для хорошо успевающих учащихся, углубляя имеющиеся знания и расширяя кругозор.
К сожалению, эти программы не всегда доступны и дорогостоящи, кроме того, в школьных программах не всегда выделяется время на их освоение. Мне кажется, более целесообразным использовать при обучении предмету программы не узко направленные, специализированные, а универсальные, многофункциональные, демонстрирующие возможность использования ПК в различных сферах деятельности человека. Я считаю интересным использование при изучении математики программного приложения MS EXEL как наиболее распространённого и доступного для всех учащихся, имеющих компьютер. В учебном процессе MS EXEL может быть как объектом изучения, так и средством обучения. При первом, усвоение знаний, умений и навыков ведёт к осознанию возможностей компьютера, а также его использование при решении разнообразных задач (компьютерная грамотность). При втором — компьютер является мощным средством повышения эффективности обучения математике: позволяет освободить учащихся от рутинного труда (громоздких вычислений), тем самым, экономя время на отработку необходимых навыков, углубляя имеющиеся знания, позволяет вникнуть в суть математических задач, показать логику, рациональность способов решения, расширяя кругозор учащихся, позволяет добиться более высокого уровня наглядности учебного материала.
В старших классах MS EXEL успешно можно использовать при изучении таких тем программы по математике:
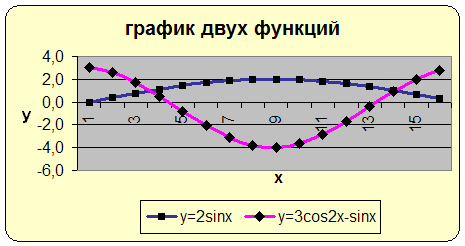
«Свойства тригонометрических функций и их графики» - учащиеся должны хорошо усвоить вид графиков тригонометрических функций, научиться определять свойства функций по графику и выполнять эскизы графиков по их свойствам. MS EXEL упрощает эту задачу и позволяет сэкономить время на отработку необходимых навыков.
«Применения непрерывности и производной» - MS EXEL позволяет показать суть решения уравнений методом деления отрезка, делает решение более наглядным.
«Решение задач на нахождение наибольшего и наименьшего значений функции» - MS EXEL позволяет подготовить учащихся к восприятию темы, решение задач по данной теме с помощью MS EXEL носит пропедевтический характер.
«Показательная функция и её график», «Логарифмическая функция и её график», «Графики тригонометрических функций» - MS EXEL способствует более прочному усвоению вида графиков функций, их свойств. Кроме того, MS EXEL даёт более высокий уровень наглядности при введении понятия обратной функции (свойств графиков взаимно-обратных функций).
MS EXEL можно широко использовать при решении уравнений и систем уравнений, которые учащиеся решают на протяжении всего курса математики в 10-11 классах.
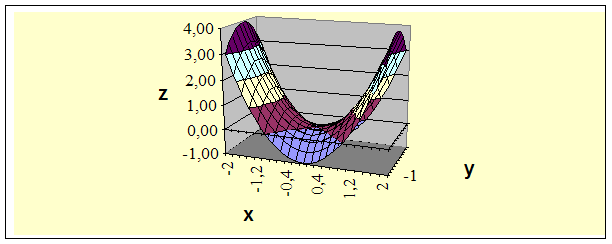
MS EXEL позволяет добиться более высокого уровня наглядности учебного материала при изучении темы «Поверхности» в курсе стереометрии.
MS EXCEL ориентирован на управление процессом обучения, позволяет учителю последовательно задавать те или иные вопросы, определять уровень усвоения материала, выявлять допущенные ошибки и в соответствии с этим вносить необходимые коррективы в процесс обучения.
MS EXCEL обладает демонстрационными функциями, даёт возможность получить красочные иллюстрации к излагаемому учителем материалу.
MS EXCEL позволяет вырабатывать набор задач определённого типа по заданной теме, обеспечив каждому учащемуся отдельное задание, соответствующее его индивидуальным возможностям.
MS EXCEL даёт возможность учащимся самостоятельно ставить и решать задачи с помощью компьютера.
На уроках мы рассматриваем задачи, решение которых с помощью MS EXCEL позволяет получить наглядное, доступное для понимания учащимися решение, показать его логику, рациональность. Попутно учащиеся получают устойчивые навыки работы с программой. Значение имеет такая последовательность рассмотрения тем: решение уравнений, решение систем уравнений, построение графиков функций, построение поверхностей и численное моделирование. При решении уравнений учащиеся приобретают умения и навыки создания и работы с электронными таблицами, отрабатывают умение пользоваться функцией ~ Подбор параметра~. Рассматривая системы уравнений, учащиеся, используя умения, полученные при изучении предыдущей темы, приобретают умение использовать функцию ~Поиск решения~. Особое значение имеет использование MS EXCEL при построении графиков функций. С одной стороны, при непосредственным построении графика учащиеся отрабатывают полученные при изучении предыдущих тем умения пользоваться функциями MS EXCEL и познакомиться с новой функцией ~Мастер диаграмм~. С другой стороны, пользуясь изображением графиков функций, изучать их свойства, сравнивать свойства различных функций.
MS EXCEL позволяет добиться более высокого уровня наглядности, особенно эффективно можно использовать наглядные возможности этой программы при изучении темы «Поверхности» в геометрии.
Одна из задач – научить школьников использовать электронные таблицы для проверки правильности построения математической модели. Электронная таблица выполняет не только функцию автоматизации вычислений. Она является очень эффективным средством проведения численного моделирования ситуации или объекта, для математического описания которых (то есть построения математической модели) используется ряд параметров. Часть этих параметров известна, а часть рассчитывается по формулам. Меняя во всевозможных сочетаниях значения исходных параметров, учащиеся могут наблюдать за изменением результатов и анализировать их. При решении задач численного моделирования учащиеся получают возможность применять полученные навыки работы с программой в новой творческой ситуации.
Задача 1.
Определение максимального объема коробки.
Имеется квадратный лист картона со стороной a. Из листа делают коробку следующим образом: по углам вырезают четыре квадрата и склеивают коробку по сторонам вырезов. Определить, какова должна быть сторона вырезаемого квадрата, чтобы коробка имела наибольшую вместимость.
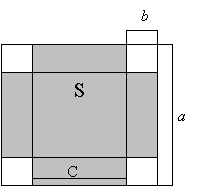В задаче рассматривается процесс преобразования одного объекта (картонного листа) в другой (коробку). Исходный объект – картонный лист – имеет заданные геометрические размеры: длина стороны а. Созданный объект – коробка характеризуется объемом, а вырезы – размером стороны и площадью.
Математическая модель.
Расчетные формулы:
С = а-2b – длина стороны дна; S = c2- площадь дна; V = Sb- объем.
Здесь а – длина стороны картонного листа, b – длина выреза.
Составьте таблицу расчета со столбцами Длина выреза, Длина стороны, Площадь дна, Объем как показано ниже. Длину выреза изменяйте с шагом 1 см.
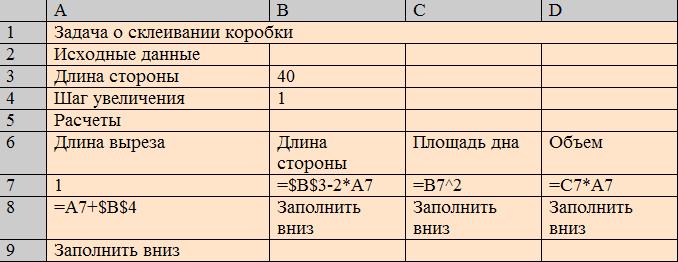
Заполнить вниз пока длина выреза не будет равна 20, а длина стороны равна Составьте геометрическую и математическую модели. Провести расчеты.
С учащимися рассматривался более сложный пример составления и решения математической модели.
Задача 2. Определение численности населения.
Чему была равна численность населения России в 2000 году?
Для решения задачи нужно иметь функцию, выражающую зависимость численности населения от времени C=f(t). Эта функция зависит от многих факторов (уровня жизни, морали, политической обстановки и т.д.) и неизвестна. Обобщив демографические данные, можно получить общий вид функции f(t): С=аеbt (1).
Здесь е – основание натурального логарифма, а, b – коэффициенты, имеющие разные значения для разных стран, t =G–1900, G – год.
Как правило, эта формула лишь приближенно отражает реальность. Одна¬ко слишком большая точность и не нужна. Будет хорошо, если численность населения будет вычислена с точностью до нескольких миллионов.
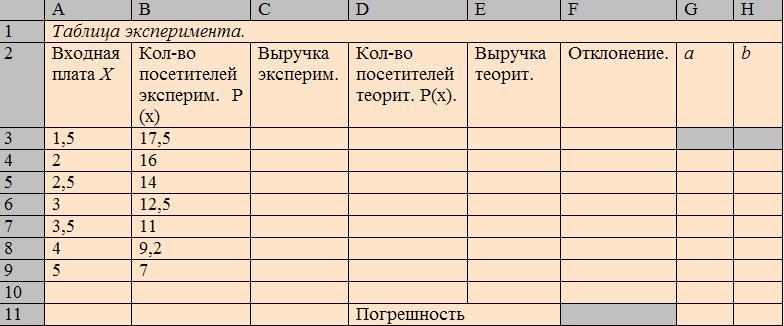
Значения функции f(t) для ряда лет можно получить из статистического справочника. Зная эти данные, можно приближенно подобрать коэффициенты а и b и затем вычислять численность населения в те годы, для которых статистических данных нет. Подбирать коэффициенты а и b нужно так, чтобы теоретические значения, вычисленные по формуле (1), не очень сильно отличались от данных статистических данных (т.е. максимальное отклонение теоретических результатов от фактических данных не должно быть слишком большим). Каждое из отклонений - это модуль разности двух чисел: фактического и соответствующего теоретического значения f(t). Максимальное отклонение называют погрешностью. Очевидно, при нахождении a и b нужно стремиться, чтобы погрешность была наименьшей.
Итак, математическая модель процесса изменения численности населения такова:
Зависимость численности населения от времени выражается формулой С=aebt (1);
Коэффициенты a=const; b=const для не очень большого промежутка времени (30–40 лет);
Значения а и b получим, минимизировав погрешность между фактическими и теоретическими данными для численности населения.
Исходные данные возьмем из статистического справочника за период с 1960 по 1995 годы (60? t ?95).
Запишем исходные данные и математические соотношения, входящие в модель, в электронную таблицу и начнем процесс численного моделирования исследуемой ситуации, т.е. подбор коэффициентов а и b в формуле (1) и определение численности населения.
Задача 3.
Определение наибольшей выручки.
Несколько человек решили организовать видео кафе на 6 столиков по 4 места за каждым. С каждого посетителя будет взиматься плата за сеанс видеофильма и ужин (всем посетителям будет предлагаться один и тот же набор блюд). Администрация города постановила, что плата за вход не должна превышать 5 $. Требуется определить такую входную плату, при которой будет получена наибольшая выручка.
Казалось бы, здесь и решать нечего. Разве не ясно, что чем больше входная плата, тем больше выручка. Вот и ответ: входная плата должна быть 5 $. Очень часто планирующие органы подобным образом и поступают. В нашем случае, если сильно увеличить входную плату, то люди перестанут посещать кафе.
Начать надо, как всегда, с построения математической модели. В чем были причины нашей неудачи? Мы предположили, что посещаемость не зависит от входной платы, и получили модель задачи, не соответствующую действительности. Значит, надо предполагать, что посещаемость зависит от входной платы.
Обозначим входную плату через X. Тогда среднее число посетителей видео салона является функцией от Х. Обозначим эту функцию через Р(Х). В задаче требуется найти такое значение X, при котором выручка, равная произведению входной платы на количество посетителей Х * Р(Х), достигает максимума. Если бы функция Р(Х) была известна, то найти требуемый максимум не составило бы особого труда. Но эта функция не известна, поэтому попробуем найти хотя бы общий вид функции. Его можно указать, обобщив опыт работы подобных кафе:
(1)
Коэффициенты а, b и с для каждого кафе свои. Как же их определить? Проще всего найти значение с. Представьте себе невообразимое - в видео кафе
пускают бесплатно (т. е. X=0). Ясно, что свободных мест не будет. Следовательно, Р(0) равно числу мест в кафе. С другой стороны, подставив 0 вместо X, получим P(0)=с. Значит, с равно количеству мест. В нашем случае с=24 (6 столи¬ков по 4 места за каждым).
Определить а и b так же просто не удается. Справочников по посещаемости видео кафе еще нет. Поэтому здесь требуется эксперимент.
Достаточно открыть кафе и установить на некоторый срок (дней на десять) определенную плату за вход. Среднее число посетителей и даст нам (приближенное!) значение функции. Установив другую плату за вход, найдем приближенное значение Р(Х) при новом X, и так несколько раз.
Зависимость посещаемости от входной платы (на основе экспериментальных данных для конкретного кафе):
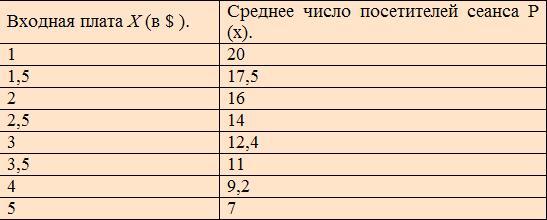Пользуясь электронной таблицей, можно подобрать значения а и b следующим способом: минимизацией погрешности между экспериментальной и теоретической выручкой. Затем можно определить, при какой входной плате выручка будет наибольшей.
Составьте следующую таблицу.
Транспортная задача
Широкий класс задач приводит к поиску оптимального значения целевой функции, которая представляет собой линейную функцию нескольких переменных. К этому классу относится транспортная задача. Многие задачи, не являющиеся транспортными по физическому смыслу, в математической модели подобны им. Таковы, например, задачи оптимального распределения финансов, кредитов, производства между предприятиями, посевных площадей, задачи о назначениях, закреплении механизмов за видами работ и др. Решение транспортной задачи является основой решения всех перечисленных задач.
Транспортная задача формулируется следующим образом: имеется m пунктов поставки и п пунктов потребления некоторого продукта. Для каждого пункта поставки задан имеющийся запас Ат продукта, а для каждого пункта потребности задан объем Вп потребностей. Известна также стоимость перевозки стп (тариф) из каждого пункта поставки в каждый пункт потребления единицы продукта. Требуется составить план перевозок с минимальной стоимостью.
Транспортная задача, в которой сумма запасов равна сумме потребностей, т. е. ?Аm = ?Вn, называется задачей с закрытой моделью. Если же это равенство не выполняется, то говорят, что задача имеет открытую модель.
Стоимость перевозки от m-го поставщика к n-му потребителю равна произведению хтп*стп, где хтп – перевозимое количество продукта.
Стоимость всех перевозок равна сумме стоимостей всех частичных перевозок ?хтп*стn, эту сумму и принимают за целевую функцию, для которой требуется найти минимальное значение.
Представим эту задачу в табличной форме:
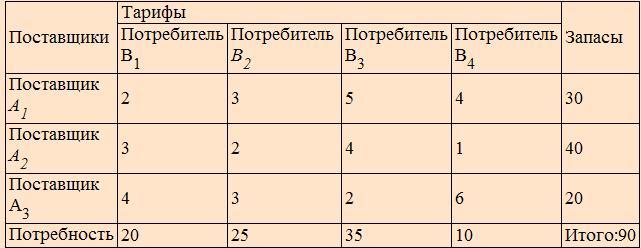Здесь в каждой из первых трех строк указаны поставщик, тарифы на перевозку к каждому потребителю и величина запаса. B нижней строке указаны потребности, причем сумма по строке "Потребность" равна сумме по столбцу "Запасы". Общая стоимость перевозок равна сумме стоимостей всех перевозок, то есть сумме произведений соответствующих тарифов на перевозимые количества продукта. B явном виде ее можно записать так:
F=2x11+3x12+5x13+4x14+3x21+2x22+4x23+1x24+4x13+3x32+2x33+6x34
Величины хтт являются искомыми переменными, а вся сумма – целевой функцией, минимальное значение которой надо найти.
Для решения задачи необходимо придерживаться определенного алгоритма действий:
1. Создать таблицу с исходными числовыми данными и рабочую таблицу с изменяемыми ячейками, в которые будут записываться получаемые результаты.
2. Составить формулу для целевой функции.
3. Указать адреса исходных и изменяемых данных, ограничения на переменные величины.
4. Сохранить полученные результаты и отчеты для анализа решения.
Исследовательская работа:
Предлагается учащимся самостоятельно рассмотреть открытую модель транспортной задачи.
Вариант 1.
Запасы поставщиков больше потребностей.
Вариант 2.
Запасы поставщиков меньше потребностей.
Далее предлагается сравнить планы перевозок обоих вариантов транспортной задачи открытой модели с планом перевозок при использовании закрытой модели. В результате можно сделать обобщающий вывод:
Общая стоимость перевозок уменьшилась (либо при полностью удовлетворенном спросе, либо при полностью использованных запасах);
В оптимальном плане произошло перераспределение перевозок из ячеек с большим тарифом в ячейки с меньшим тарифом;
Либо запасы реализованы не полностью, либо потребности удовлетворены не полностью.
Предложенный подход к решению задач дал положительные результаты:
Увеличилась активность на уроках, учащиеся не только с удовольствием выполняют задания учителя, но и выступают со своими предложениями, придумывают ситуации, ставят задачи и продумывают пути их решения.
Реализация этих идей в старшей школе обусловлена современными требованиями общества к развитию творческой личности. В основном эти требования направлены на формирование готовности учащихся к профессиональному самоопределению
|
Школа-лицей № 320 
